Mit nur zwei Farben angefärbte Würfel gibt es nur 10, wenn man von Rotationen absieht.
Wenn man von Rotationen nicht absieht sind es 2^6 = 64.
Ich zeige sie hier am abgewickelten Würfel.
Diese Abzählungen kann man mit dem Lemma von Burnside elegant ausführen.
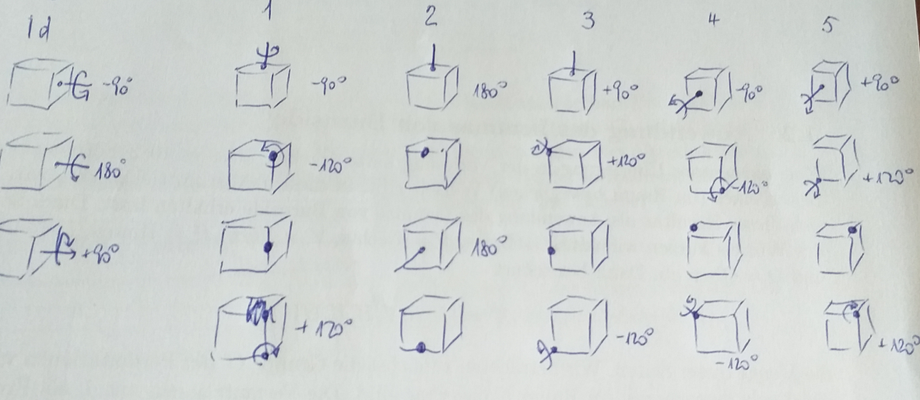
Beim Würfel gibt 24 verschiedene Rotationen. Ich zeige sie in der angehängten Illustration 2.
Wie diese 24 Rotationen auf die sechs Würfelseiten (Vorne, Hinten, Links, Rechts, Unten und Oben) auswirken ist in Illustration 10 gezeigt. Dabei ist U,O,RHLV die Zyklenschreibweise und
bedeutet U und O bleiben an Ort und R geht nach H, H nach L, L nach V und V nach R.
Entscheidend ist die Zyklenanzahl m, weil alle Elemente eines Zyklus eine einheitliche Farbe bekommen. Wenn m k mal vorkommt so ist das der Koeffizient in der Formel ... + k * f^m + ...
Burnside besagt nun, es gibt von Rotationen abgesehen n Würfel mit maximal f Farben
n=1/24*(f^6+3*f^4+12*f^3+8*f^2).
Bei f=2 Farben ergibt die Formel 10.
Wenn man statt dessen die Wirkung der Rotationen auf die Kanten (labeling siehe Illustration 3) des Würfels betrachtet, kommt man auf die Formel
n=1/24*(f^12+6*f^7+3*f^6+8*f^4+6*f^3)
Man kann die Kanten eines Würfels auf diese n verschiedene Weisen mit maximal f Farben anfärben.
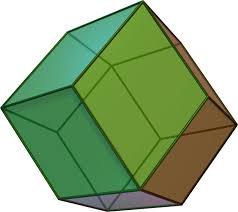
Für das Rhombendodekaeder (Illustration 5) gilt das gleiche n.
Wenn man statt dessen die Wirkung der Rotationen auf die Ecken (labeling siehe Illustration 4) des Würfels betrachtet, kommt man auf die Formel
n=1/24*(f^8+17*f^4+6*f^2)
Für das Oktaeder gilt das gleiche n.
Man kann Seiten, Kanten und Ecken auch kombinieren, die k's zu gemeinsamem m müssen dann addiert werden.
So kommt man zu Formeln
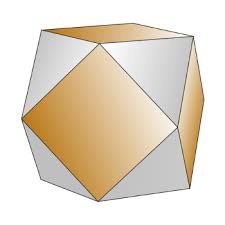
für das KubOktaeder (Seiten und Ecken; Illustration 6)
n=1/24*(f^14+3*f^8+6*f^7+8*f^6+6*f^5)
für das 4-truncated Rhombendoekaeder (Kanten und Seiten; Illustration 7)
n=1/24*(f^18+9*f^10+14*f^6)
für das 3-truncated Rhombendoekaeder (Kanten und Ecken; Illustration 8)
n=1/24*(f^20+6*f^11+3*f^10+8*f^8+6*f^5)
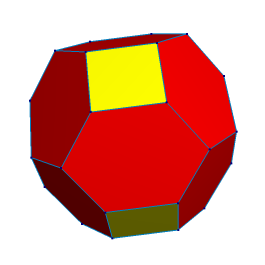
für das RhombenKubOktaeder oder Truncated KubOktaeder (Seiten, Kanten und Ecken; Illustration 9 und 10)
n=1/24*(f^26+9*f^14+8*f^10+6*f^8)
 Baumann Eduard
Baumann Eduard